Une ressource pour l'option Mathématiques complémentaires : Une séquence articulant les thèmes "Calculs d'aires" et "Temps d'attente"

• Dossier complet à télécharger [zip] (fichiers GeoGebra, doc, pdf)

• Tuto sur la construction d'histogramme sur GeoGebra [pdf]

Le premier problème, que nous appelons le problème de la rencontre, est une adaptation d'un exercice d'application proposé dans le document Ressources Probabilités et statistiques de la classe de terminale (MENJVA, 2012). L'énoncé est cependant beaucoup plus ouvert que dans l'exercice original.

L'énoncé du problème proposé aux élèves est le suivant :

La résolution de ce problème se fait par une réflexion collective des élèves (en classe entière et/ou en petits groupes). Il n'est pas prévu que les élèves s'emparent du problème de façon individuelle, c'est au contraire le collectif qui va mettre en place une démarche de modélisation pour arriver au choix d'une courbe de densité (que les élèves appelleront dans un premier temps « courbe de tendance »). Une démarche de modélisation étant attendue, les élèves doivent se mettre d'accord pour faire des choix. Bien entendu, plusieurs modélisations sont possibles avec ce problème et plusieurs démarches aussi. Cependant, pour l'objectif d'enseignement que nous avons, nous espérons que les élèves partent dans une certaine direction, que nous détaillons ensuite.

Un des premiers choix à faire est de savoir si l'on considère le temps comme un phénomène discret ou continu. Ici, le problème amène assez naturellement à considérer le temps comme un phénomène continu. De plus, de manière assez immédiate les élèves considèrent que Karine et Olivier arrivent de façon indépendante et peuvent arriver de façon uniforme sur l'intervalle de temps considéré. Cela permet donc de considérer deux variables aléatoires \(T_K\) et \(T_O\) représentant respectivement les moments d'arrivée de Karine et Olivier suivant toutes les deux une loi uniforme sur \([7 ;8]\) (cela revient au même de les considérer sur [0 ;1]). Le temps d'attente du premier arrivé est alors la variable aléatoire \(X=|T_K-T_O |\) à valeurs dans \([0 ;1]\) (on pourrait aussi faire le choix d'exprimer les temps en minutes et donc de considérer l'intervalle [0;60]). On cherche alors la loi que suit cette variable aléatoire. Dans le document Ressources, c'est une résolution géométrique qui est proposée. Ici, cela donnerait :

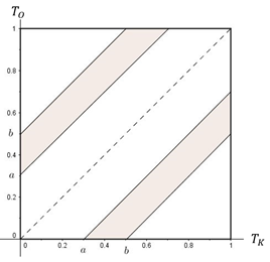
Cette solution permet de définir, pour tous \(a\) et \(b\) appartenant à \([0 ;1]\) tels que \(a \leq b\), la probabilité \(P(a \leq X \leq b)\) comme étant l'aire des parties colorées ci-dessus. En effet, les parties colorées correspondent à l'ensemble des points de \([0;1]^2\) tels que \(a \leq |T_K-T_O | \leq b\). Cette démarche, correcte bien entendu, ne permet cependant pas d'arriver à la notion de fonction de densité, ce qui est l'objectif ici. Au cours des années où ce problème a été expérimenté, elle n'a jamais été proposée par les élèves.

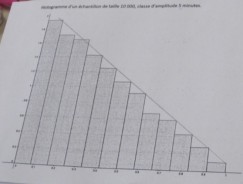
La démarche espérée est que les élèves proposent de faire des simulations, sur tableur par exemple, pour avoir un (ou des) échantillon(s) de taille suffisamment grande (10 000 par exemple). La formule pour simuler l'expérience aléatoire à entrer est =ABS(ALEA()-ALEA()) sur tableur ou =Abs(Random()-Random()) sur le tableur du logiciel GeoGebra . Inspirés par la démarche du problème du point mobile du devoir maison, les élèves peuvent ensuite penser à représenter les données sous forme d'histogramme, avec des amplitudes plus ou moins grandes.

Ci-dessus : Histogrammes d'un échantillon de taille 10 000 avec des classes d'amplitudes 15 minutes (à gauche) et 5 minutes (à droite)

Une fois les histogrammes construits, les élèves doivent déterminer une « courbe de tendance » (comme dans le problème du point mobile). La contrainte de proximité avec le haut des rectangles ne suffit pas, car l'aire sous cette courbe va permettre de calculer des probabilités. Il faut pour cela que les élèves prennent conscience du fait que l'on a besoin de contraintes supplémentaires pour déterminer l'expression de la fonction affine décroissante qu'ils cherchent, notamment que l'aire sous la courbe sur \([0;1]\) doit valoir 1. De plus, au regard de l'histogramme, on peut imposer \(f(1)=0\). Ce choix est raisonnable car on observe que si l'on réduit de plus en plus l'amplitude des classes de l'histogramme, la densité de fréquence sur une classe de la forme \([1-\epsilon ;1]\) (avec \(\epsilon\) très petit) est presque nulle .

On arrive alors à la fonction \(f(x)=-2x+2\) sur \([0;1]\). La connaissance de cette fonction permet de connaître la probabilité que le temps d'attente soit dans n'importe quel intervalle de \([0;1]\), ce qui répond au problème posé.

Nous poursuivons la séance par l'exercice d'application ci-contre, qui permet aux élèves de prendre conscience que maintenant à l'aide de calculs d'aire sous la courbe qu'ils ont trouvée (aires de triangles et de trapèzes), ils peuvent déterminer toutes les probabilités qu'ils veulent. Cet exercice permet aussi de travailler sur l'écriture symbolique probabiliste d'événements.

Cette recherche se déroule sur une "séance" de 2 ou 3 heures. Tout le travail sur le logiciel GeoGebra se fait en classe entière avec un seul ordinateur vidéoprojeté qui est manipulé par l'enseignante ou par les élèves. Les élèves terminent l'exercice d'application à la maison ou en classe suivant la modalité choisie.

Ici, nous présentons une modalité où le travail est individuel et en classe entière. Il est tout à fait envisageable de proposer un travail en groupe, même si un temps en classe entière est souvent indispensable pour enclencher la simulation.

Dans un premier temps, les élèves ont une phase de recherche individuelle. Le fait que la question soit très ouverte peut en bloquer quelques-uns, mais ils finissent tous par avoir quelques remarques à dire. Une première mise en commun permet d'engager des discussions dans la classe sur plusieurs points, que nous allons illustrer. Dans cette phase, l'enseignant écrit au tableau toutes les idées des élèves, qui sont invités à prendre des notes tout au long de la séance.

Illustration de discussions en classe

Les élèves discutent de la vraisemblance ou non du problème :

Élève 1 : Je disais que c'est un peu bizarre comme rendez-vous... [...] On se donne pas rendez-vous entre 7h et 8h...

L'enseignante peut au bout d'un moment recentrer le travail :

P : Alors bon, peut-être, se donner rendez-vous entre 7h et 8h, c'est une plage horaire relativement grande... mais aussi pour que ce soit plus facilement traitable pour nous. On aurait pu se dire « ils se donnent rendez-vous entre 7h et 7h15 », est-ce que ça changeait ce qu'on va... est-ce que ça changeait le problème ?

Les élèves arrivent au caractère aléatoire de la situation et se questionnent sur le caractère discret ou continu du temps :

Élève 2 : Si on considère qu'il y a autant de chance qu'ils arrivent à... chaque minute... entre 7h et 8h... donc ils ont une chance... en fait... Karine a 1 chance sur 60 d'arriver à... x heure... donc ils ont un soixante... un sur soixante au carré...

[...]

Élève 3 : Moi je dirais que c'est... on parle pas en minute, là on parle à tout moment donc... je dirais que même les secondes, il y a déjà beaucoup plus de... Par exemple, si on arrive à 7h28min37s, c'est pas pareil. En plus, il y a les millièmes de seconde et...

Plusieurs élèves : Et les milliards de seconde.

Élève 3 : Et les milliardièmes de seconde après.

Élève 4 : C'est comme la puce hier [l'élève fait référence au problème du point mobile].

Élève 3 : Oui, c'est infini en fait.

P : Ah, c'est comme la puce.

Élève 3 : Oui, c'est comme la puce.

Élève 5 : Sauf que...

Élève 1 : Sauf que c'est des minutes...

Élève 3 : Oui, mais c'est comme la puce.

Élève 4 : Quand t'arrives... quand t'arrives à 7h31 et que l'autre arrive à 7h32...

Élève 4 : Non à 7h31 virgule zéro cinq et 7h virgule trente-deux, t'es à la même heure.

Élève 1 : Oui, mais on est en maths.

P : Ah ! « Mais on est en maths ».

[...]

Élève 4 : C'est... Il y a une possibilité infinie de... d'arriver... enfin... [...] Entre 8... entre 7h et 8h, on a une possibilité infinie d'arriver à une certaine heure.

P : Une infinité de moments tu veux dire ? d'instants ?

Lors des différentes années d'expérimentation, la modélisation par une variable aléatoire continue a toujours fini par être retenue.

Des considérations qualitatives peuvent alors suivre, comme par exemple : le temps d'attente est entre 0 et 1 heure, il y a plus de « chance » que le premier arrivé attende 5 minutes que 55 minutes...

Une fois les remarques qualitatives épuisées, il faut souvent relancer la recherche.

De façon informelle en Mathématiques complémentaires, les variables aléatoires \(T_O\) et \(T_K\) représentant respectivement les heures d'arrivée d'Olivier et Karine sont introduites par les élèves (ou par l'enseignant) et la variable aléatoire représentant le temps d'attente \(X\) est définie par \(X=|T_O-T_K|\).

Les élèves peuvent proposer de prendre un exemple : calculer la probabilité que le temps d'attente du premier arrivé soit inférieur à 10 minutes. Ayant rencontré, dans le problème du point mobile, des simulations ensuite mise sous forme d'histogramme, les élèves proposent assez naturellement (bien que cela puisse mettre du temps) de simuler des réalisations de la variable aléatoire \(X\) et ensuite de les représenter sous forme d'histogramme.

Un temps est laissé aux élèves pour chercher la formule à entrer dans le tableur pour simuler des réalisations de la variable aléatoire \(X\). L'utilisation du logiciel GeoGebra pour construire les histogrammes est amenée par l'enseignante.

Suivant les classes, l'idée de chercher la « courbe de tendance » (vocabulaire employé dans le problème du point mobile) est plus ou moins immédiate :

P : Si je vous demandais de... avec ça, de... d'évaluer le... la probabilité que le temps d'attente soit entre 0,2 et 0,3. D'accord ? Imaginons. Comment vous feriez ?

P : Est-ce que c'est bien ça qu'on essaie d'évaluer ? La probabilité que le temps d'attente soit entre tant et tant ? Donc si je vous demandais ça... Si je vous posais cette question « évaluer le temps d'attente entre 0,2 et 0,3 », comment vous feriez avec cet... à l'aide de cet histogramme ?

[...]

Élève 5 : Entre 0,2 et 0,3 ?

P : Oui. Juste, comment tu ferais, pas ce que tu trouverais. Mais comment tu ferais ?

Élève 5 : On peut faire comme dans le DM, c'est-à-dire... on peut tracer une courbe de tendance. On va pouvoir calculer l'aire de ce triangle... et puis prendre une amplitude qui correspond à 0,2 ~ 0,3.

Ici, on remarque que l'élève a bien identifié les différentes étapes de la démarche (bien que cela ne soit pas nécessairement exprimé de la « bonne façon »). Les élèves sont tous d'accord qu'il s'agit d'une droite (plus exactement d'un segment). Un temps individuel est ensuite laissé aux élèves pour déterminer cette (ces ?) courbe(s) de tendance. Dans un premier temps, les élèves proposent des courbes en reliant « le haut des rectangles aux extrémités » ou en reliant le haut du rectangle sur l'axe des ordonnées et le point extrême d'abscisse 1 ou encore un segment « à vue d'œil » coupant les rectangles de façon équilibrée pour qu'il y ait « autant de vide en-dessous que de bout de rectangles au-dessus ».

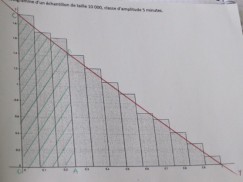
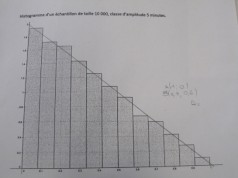
Une mise en commun est nécessaire pour amener les élèves à prendre conscience des contraintes que doit vérifier cette fameuse courbe de tendance. Il émerge rapidement que l'aire sous la courbe doit être égal à 1. Ensuite, les élèves proposent parfois \(f(0)=2\), mais cette contrainte est moins « justifiable » que \(f(1)=0\) (cf. présentation du problème). On insiste alors avec les élèves sur le fait que nous faisons un choix de modèle.

Deux possibilités :

- Les élèves ont ensuite une synthèse de la séance à rédiger, pour faire ressortir les différentes étapes de la démarche qu'ils ont faite en classe. L'enseignante propose ensuite un résumé de leurs synthèses.

- La synthèse est faite par l'enseignante.

Cela n'est pas forcément visible dans l'écrit mais il est important qu'au moins à l'oral toutes les propriétés de la fonction de densité qui apparaissent dans la synthèse soient justifiées par les élèves lors de la séance.

Il n'est pas indispensable d'introduire le vocabulaire « fonction de densité de probabilité » à la fin de cette séance (cela n'est pas fait dans cette synthèse). Cependant les élèves peuvent déjà tout à fait justifier ce choix de vocabulaire. Voici la réponse d'un élève (expérimentation 2015) quand l'enseignante demandait de justifier le vocabulaire :

E1 : C'est parce que sur l'axe des ordonnées, c'est la densité.

Les autres élèves acquiescent en se remémorant le travail mené sur l'histogramme, où il est fortement question du fait que l'axe des ordonnées pour un histogramme représente la densité de fréquence.

Pour justifier la positivité de la fonction de densité puis le fait que l'aire sous la courbe est égale à 1, on retrouve à nouveau une justification prenant appui sur l'histogramme :

E2 : Parce qu'en fait c'est par rapport à l'histogramme donc on peut pas avoir de rectangles en-dessous.

E3 : Parce que ça correspond à la fréquence. L'aire correspond... [...] L'aire correspond à la somme de toutes les probabilités... [...] La somme des fréquences.

P : Et donc on sait que ça fait...

E3 : Un.