Problème du point mobile
Fondamental : Objectifs
Les objectifs de cette séance sont de :
Découvrir une démarche de modélisation faisant intervenir une variable aléatoire continue
Découvrir la notion de "courbe de tendance" qui deviendra au cours des séances suivantes la courbe de densité
Étudier (sans le dire explicitement) une loi uniforme sur un intervalle.
Documents à télécharger
Énoncé du problème : en pdf [pdf]
Ce problème peut être traité sur 1h ou 1h30 suivant les modalités (travail en autonomie ou travail en groupe avec restitution écrite).
Le problème du point mobile est une première rencontre avec une loi uniforme continue. La loi uniforme ne sera cependant pas institutionnalisée à ce moment-là. L'exercice est une adaptation d'une situation proposée par un groupe IREM d'Aquitaine (Barbazo et al., 2003) :
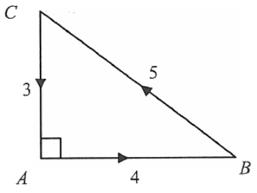
Un point mobile M se déplace à vitesse constante sur le « pourtour » d'un triangle, toujours dans le même sens (indiqué par la flèche). On suppose qu'il démarre au point C. Une panne se produit subitement et aléatoirement et le point mobile s'arrête instantanément.
Le problème a ici été pensé en plusieurs étapes : une première phase de conjectures, où les élèves peuvent répondre de façon intuitive ; une deuxième qui s'appuie sur la simulation pour évaluer les probabilités à partir des fréquences observées sur l'histogramme donné ; et une troisième basée sur des calculs théoriques prenant appui sur une « courbe de tendance » qui a été déduite des quatre histogrammes fournis. Cette courbe étant celle qui « lisse » les histogrammes (la même pour les quatre histogrammes).
Remarque :
Introduire la notion de fonction de densité dans le cas de la loi uniforme continue n'est, selon nous, pas le plus pertinent car comme le montre la première partie de cet exercice, les calculs peuvent être faits par les élèves de façon intuitive et donc le besoin d'une courbe de densité n'est pas réel. Cependant, ce problème permet aux élèves de rencontrer une certaine démarche de modélisation et de concevoir une « courbe de tendance » qui lisse les histogrammes, et de rencontrer la problématique de \(P(X=a)=0\). Cela sera utile pour le problème de la rencontre et le problème du volcan Aso.
Fondamental : Synthèse
Il faut retenir de ce problème les différentes étapes de la démarche de modélisation, notamment :
utiliser le tableur pour simuler des réalisations d'une variable aléatoire,
représenter les réalisations obtenues sous forme d'un histogramme de fréquences,
rechercher une "courbe de tendance" qui permettent de lisser tout histogramme de fréquences qui représente des réalisations de cette variable aléatoire,
calculer des probabilités à partir de cette courbe.
Ces idées ne doivent pas forcément être formulées dès cette étape, mais elles seront importantes pour le bon déroulement du problème de la rencontre (au moins en acte).
Les élèves doivent aussi retenir la commande =ALEA() sur le tableur pour simuler le choix au hasard d'un nombre "réel" entre 0 et 1.
Des éléments sur le déroulement possible en classe
Deux modalités ont été testées :
- une modalité en classe entière avec un travail collectif (dans le cas d'une classe à dominante économiste, peu familière avec les simulations)
- une modalité en travail de groupe pendant une heure avec restitution écrite sur une séance, puis débat de 30 minutes guidé par l'enseignante avec appui sur les productions des élèves sur une autre séance.