Problème du volcan Aso
Fondamental : Objectifs
Les objectifs de ce problème sont :
dans un premier temps, de réinvestir les propriétés de la fonction de densité pour continuer de donner du sens à cette notion et,
dans un second temps, d'introduire le calcul approché d'aire.
Documents à télécharger
Énoncé du problème du volcan Aso [pdf] (et documents élèves)
Dossier complet à télécharger [zip] (fichiers GeoGebra, doc...)
Le problème du volcan se déroule sur 2h ou 3h (si l'on va jusqu'à la mise en place de la méthode de calcul approché d'aire).
Rappel :
Le problème du volcan Aso a lieu lors de la séance qui suit le problème de la rencontre. Il faut garder en tête que les élèves n'ont pas encore rencontré le calcul intégral.
Ce problème s'appuie cette fois-ci sur des données réelles, que l'on trouve dans le manuel Math'x (2012). Elles ont cependant été complétées (le site http://volcano.si.edu/volcano.cfm?vn=282110 recense l'ensemble des dates d'éruptions de ce volcan).
Le volcan Aso est un volcan actif qui est régulièrement en éruption ces dernières années : lien 1 lien 2 lien 3
L'énoncé distribué aux élèves est le suivant :
Le volcan Aso, situé sur l'île de Kyushu au Japon, est l'un des volcans les plus actifs au monde. On possède un relevé précis de ses éruptions, régulièrement tenues depuis le XIIIe siècle. Dans le tableau ci-dessous, nous disposons de ces données pour la période allant du XIIIe au XXIe siècle. Nous nous intéressons au temps écoulé, en années, entre deux éruptions successives.
Les questions posées aux élèves (qui peuvent évoluer en fonction des nouvelles éruptions) sont les suivantes :
La dernière éruption du volcan Aso a eu lieu en avril 2019. a) Comment évaluer la probabilité que la prochaine éruption ait lieu avant avril 2023 ? b) Comment évaluer la probabilité que la prochaine éruption ait lieu au cours de l'année 2031 ? |
Dans ce problème, il s'agit, à partir de données réelles sur le passé, de « prédire » l'avenir. C'est une problématique de statistique inférentielle. Pour la première question, une première évaluation peut se faire à l'aide de la fréquence qui découle des données fournies. Pour répondre à la deuxième question, il est attendu des élèves qu'ils mettent en place une démarche similaire à celle du problème de la rencontre. Ils doivent rassembler les données sous forme d'un histogramme, puis chercher une fonction de densité. Tout l'enjeu de ce problème est la détermination de cette fonction de densité, qui cette fois-ci, n'est plus une fonction affine. On espère qu'après débat dans la classe, les élèves finissent par modéliser la situation par une loi exponentielle (sans la nommer ainsi bien sûr), mais d'autres lois pourraient être choisies. Cela amènera ensuite la question : comment calculer l'aire sous une telle courbe ? Dans ce cas, nous arrivons à un calcul d'aire sous une courbe non rectiligne. Les élèves vont être alors chercher des méthodes d'approximations d'aire sous une courbe.
Plusieurs modèles du temps d'attente entre deux éruptions pourraient être envisageables. Il faut en tout cas garder en tête que le choix de modèle qui sera fait n'est autre qu'une conjecture de modèle. Il faudrait ensuite confronter cette proposition à la réalité pour la légitimer ou non, ce qui ne nous intéresse pas ici. D'ailleurs, le modèle exponentiel n'est en fait pas réellement adapté à une situation de temps d'attente dans des phénomènes naturels qui, d'après les spécialistes du domaine, ne sont pas des phénomènes sans mémoire.
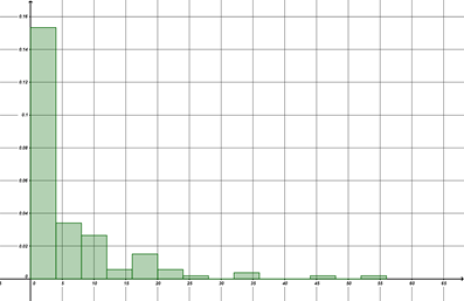
Comme pour le problème de la rencontre, une démarche de modélisation est nécessaire. Ici, nous disposons de données réelles et nous pouvons remarquer que des choix ont déjà été faits, par exemple le fait que seules les années d'éruption soient précisées et donc que les temps d'attente entre deux éruptions consécutives sont donnés en années entières. Il faut donc choisir comment considérer la donnée « \(k\) années » ? Est-elle à voir comme une donnée isolée ou comme représentant un intervalle ? Lequel ? Il est assez naturel de considérer le temps d'attente entre deux éruptions comme continu. Ce qui est sûr, c'est qu'en réalité une donnée k peut représenter n'importe quelle valeur de l'intervalle \(]k-1;k+1[\), cependant cela entraîne des chevauchements. Il faut donc faire un choix arbitraire qui ne crée pas de chevauchements. Dans l'histogramme présenté, nous avons fait le choix de considérer une donnée k comme appartenant à l'intervalle \([k;k+1[\) (étant donné que certaines valeurs valent 0). Ce questionnement n'est pas forcément abordé dans la classe, mais il est utile que l'enseignant ait conscience de cela.
Ce problème faisant suite à celui de la rencontre, il est attendu que les élèves se l'approprient facilement et proposent rapidement les différentes étapes de la démarche : représenter les données statistiques sous forme d'histogramme pour ensuite déterminer une « courbe de tendance » (courbe de densité) qui nous permettra de faire les calculs de probabilités attendues. Tout d'abord, il est nécessaire de laisser un temps individuel ou en binôme pour que les élèves commencent à manipuler les données. Il peut être intéressant de les laisser tracer eux-mêmes leur histogramme à la main. Ensuite, un histogramme doit être fait sur le logiciel GeoGebra. En effet, cela permet ensuite de tester rapidement les fonctions de densité candidates pour vérifier la cohérence visuelle avec l'histogramme, de vérifier le fait que la fonction est bien positive et de plus, la commande « Inspecteur de fonction » du logiciel permet de connaître l'aire sous la courbe entre deux bornes données. Les élèves, ne connaissant pas encore le calcul intégral, ont ce moyen pour obtenir l'aire sous la courbe. Cet histogramme sur GeoGebra est donc le point d'appui pour la discussion sur le choix de la fonction de densité.
Remarque :
Nous avons déjà souligné que les histogrammes sous GeoGebra sont à pas constants, ce qui n'est pas le plus approprié ici. Le fait qu'il y ait des « trous » dans l'histogramme peut gêner certains élèves dans la recherche d'une fonction, qui soit continue. Toutefois, les élèves ayant bien assimilé la notion d'histogramme grâce aux séances sur l'histogramme sont capables de passer au-delà :
Élève : Je pense qu'il faudrait faire un histogramme avec des classes d'amplitudes différentes pour que ça puisse prendre toutes les valeurs... Enfin pour pas qu'il y ait de trous.
Une fois l'histogramme construit, les élèves doivent se mettre d'accord sur l'ensemble de définition de la fonction de densité qu'ils cherchent. Il est attendu qu'ils choisissent \([0;+\infty[\). Avec les données dont ils disposent, les temps d'attente ne dépassent pas 56 ans, or il n'est bien entendu pas raisonnable de penser que ce temps d'attente ne peut pas être supérieur. Ce choix d'un intervalle non borné amènera la question de la possibilité d'avoir une aire finie d'un domaine infini, d'où l'importance que cette problématique ait été anticipée au préalable dans l'année lors du devoir maison consacré à cela.
Nous attendons des élèves qu'ils proposent dans un premier temps une fonction de type fonction inverse (fonction de référence bien connue des élèves) de la forme : \(\frac{a}{bx+c}\), qui peut être implémentée dans le logiciel GeoGebra avec des curseurs. Ces fonctions seront ensuite réfutées car elles ne peuvent pas vérifier toutes les conditions que l'on désire : l'aire sous la courbe sur \([0;+\infty[\) est supérieure à 1 (elle est infinie). Nous y reviendrons dans la présentation du déroulement. Cela permet aux élèves de prendre conscience de l'importance des caractéristiques des fonctions de densité, empêchant certaines fonctions d'être retenues pour ce rôle. Après avoir disqualifié ces fonctions, nous attendons que les élèves proposent une fonction du type exponentielle décroissante (qui doit donc faire partie des fonctions de référence des élèves) de la forme : \(\lambda e^{-kx}\). Avec un jeu sur les paramètres à l'aide des curseurs de GeoGebra, les élèves peuvent se mettre d'accord sur l'expression d'une fonction. Il faut noter que plusieurs choix de la forme : \(f(x)=\lambda e^{-kx}\) peuvent être proposés, avec \(k \)suffisamment proche de 0,2.
Des éléments sur le déroulement en classe
Ce problème se déroule sur une séance de 2h ou 2h30, suivant le temps laissé aux élèves dans les phases de travail individuel ou en binôme. Le travail se fait de nouveau en classe entière avec un seul ordinateur vidéoprojeté, pris en charge par l'enseignante ou un élève.
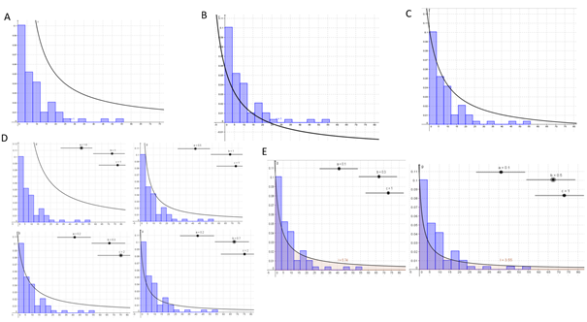
Nous reprenons ici le cheminement des élèves lors de l'expérimentation de 2015 , lors de la recherche d'une courbe de densité (cf. figure ci-dessous). Une fois l'histogramme tracé sur le logiciel GeoGebra, les élèves doivent résoudre la tâche suivante : « On cherche une fonction f définie sur \([0;\infty[\) qui approche « au mieux » l'histogramme ». La plupart des élèves proposent la fonction \(x \mapsto \frac{1}{x}\). L'enseignante décide donc de faire une mise en commun en partant de cette fonction (phase A). Cette courbe ne convenant pas visuellement aux élèves, ils décident de « la descendre ». Cependant, la fonction devient alors négative à partir d'un moment (phase B). Les élèves doivent mobiliser leurs connaissances sur la fonction de densité (la fonction doit être positive sur l'intervalle de définition) pour poursuivre leur recherche. La fonction représentée ensuite (phase C) parait positive mais ne l'est plus à partir d'un moment. Cela entraîne le fait de chercher une fonction de la forme \(f(x)=\frac{a}{bx+c}\), toujours positive sur \([0;\infty[\), d'où l'arrivée ensuite de curseurs. Le travail de recherche de la « meilleure » courbe se poursuit (phase D). Reste ensuite à prendre en compte le fait que l'aire sous la courbe doit valoir 1. Certains élèves disent que l'aire est nécessairement infinie, vu que l'on se place sur \([0;\infty[\), mais il y a toujours d'autres élèves qui contredisent cela en faisant référence au devoir maison qui les a fait travailler sur cette problématique. Ce point de blocage est donc vite écarté grâce à l'anticipation dans l'année. L'« Inspecteur de fonction » permet de connaître l'aire sous la courbe sur \([0 ;1000]\) par exemple (nous ne pourrons bien entendu pas aller jusqu'à l'infini) et les élèves s'aperçoivent que l'aire est finie mais toujours supérieure à 1 (phase E). Pour que l'aire diminue, il faut choisir des fonctions dont l'allure finit par ne plus du tout correspondre à l'histogramme.
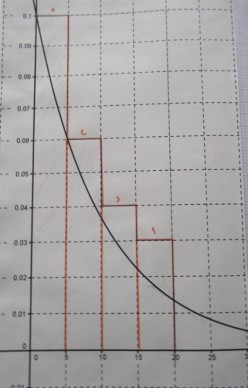
Ce long travail, indispensable pour bien consolider les propriétés de la fonction de densité, permet finalement d'invalider ces fonctions candidates. Les élèves proposent toujours ensuite une fonction du type \(f(x)=\lambda e^{-kx}\). A nouveau, un travail sur GeoGebra, avec les curseurs, permet de voir que \(\lambda\) doit être égal à \(k\) pour que l'aire soit égale à 1 et permet aux élèves de se mettre d'accord sur une expression pour la fonction. Une année où le matériel informatique n'a pas fonctionné, l'enseignante a dû imposer le paramètre λ et l'adhésion de la classe a été moindre. Il semble important que cette fonction soit le choix de la classe.
Il peut être intéressant de mentionner aux élèves que les mathématiciens qui travaillent en statistique appliquée disposent de méthodes pour choisir les paramètres les plus adaptés à leur jeu de données (par exemple, la méthode du maximum de vraisemblance). Il est aussi indispensable de leur faire prendre conscience que nous ne savons pas si le modèle choisi est « le bon », comme précisé plus tôt. Il faudrait un retour vers la réalité pour que le modèle soit validé ou non.
A la fin de cette recherche, le nouveau problème est le suivant : comment calculer les probabilités nous-mêmes ? Une seconde phase de travail démarre : comment calculer l'aire sous cette courbe entre 0 et 20 ? La courbe choisie par les élèves est distribuée à chaque binôme (le choix de donner un papier quadrillé guide les élèves vers des procédures de comptage de carreaux). Le déroulement est assez classique : un temps de recherche et une mise en commun des méthodes et des résultats trouvés. Les méthodes proposées par les élèves sont les suivantes :
Comptage de carreaux souvent seulement sous la courbe ;
Méthode de compensation : ils comptent les carreaux en dessous en découpant certains pour qu'il y ait compensation au-dessus et en-dessous ;
Méthode des trapèzes ;
Méthode des rectangles...
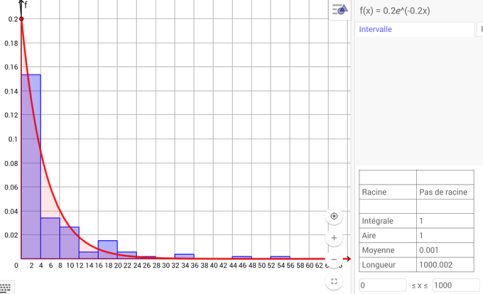
Il est important de laisser le temps à chaque binôme de trouver une réponse. Il faut que chacun ait le temps d'expérimenter sa méthode afin d'accepter aussi celles des autres et de se convaincre que certaines démarches sont meilleures que d'autres et pourront être systématisées. La méthode des rectangles est reconnue par les élèves comme la plus facile et peut ensuite être institutionnalisée et programmée. Le logiciel GeoGebra permet aisément de montrer aux élèves ce qui se passe quand le nombre de rectangles tend vers \(\infty\). Exemple avec \(f(x)=0,2e^{-0,2x}\) :
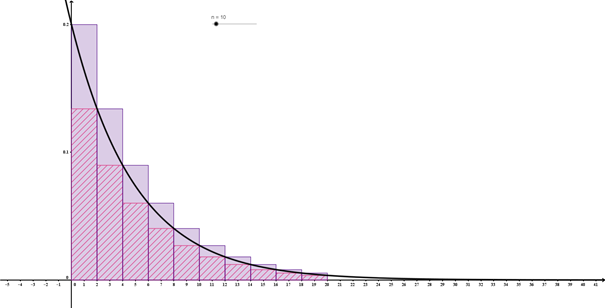
Fondamental : Synthèse
Fondamental : Institutionnalisation
A l'issue de ces séances, une institutionnalisation est nécessaire pour décontextualiser les nouvelles notions rencontrées :
fonction de densité d'une variable aléatoire continue ;
loi uniforme, loi exponentielle ;
méthode des rectangles.
Se reporter à la rubrique Cours et exercices.