Histogrammes
Fondamental : Objectifs
Une nouvelle « première » rencontre avec la notion d'histogramme doit avoir lieu pour qu'elle puisse être un point d'appui à l'émergence de la notion de fonction de densité. Pour cela, nous proposons une séance dédiée à cette notion.
L'objectif de cette séance est de :
(Ré)introduire et (re)définir la notion d'histogramme ;
Simuler un nombre réel aléatoire sur un intervalle avec un tableur (anticipation pour la séance suivante).
Documents à télécharger
Énoncé des exercices : en pdf [pdf]
Correction des exercices : en pdf [pdf]
Dossier complet à télécharger [zip] (avec les documents en version pdf, docx et tex ainsi que les fichiers xls)
Ce travail se déroule sur deux heures (travail à rendre à finir à la maison).
Présentation du premier exercice
Le premier exercice a pour objectif de réintroduire la notion d'histogramme. Nous nous appuyons sur des données statistiques sur la répartition des âges de la population parisienne en 2011 :
Avant de définir un histogramme, il nous semble indispensable de définir ce qu'est la densité de fréquence. Une analogie qui nous semble adaptée pour les élèves et que nous reprenons de Bressoud & Kahané (2010) est celle avec la densité de population. Nous reprenons leur exemple, avec des données actualisées :
D'après les dernières données, Monaco avait 37 308 habitants (en 2016) et le Japon 126 477 000 (sources :Institut Monégasque de la Statistique et des Études Économiques et Institut nationale d'études démographiques). Bien sûr, les démographes diront que ces renseignements sont très largement insuffisants pour comparer la démographie des deux pays : il faut au minimum s'intéresser aux superficies de ces deux pays et calculer pour chacun la densité de population, c'est-à-dire le nombre d'habitants au kilomètre carré. Avec une superficie de 2,02 km2 pour Monaco et de 378 000 km2 pour le Japon, les densités sont respectivement \(d_1=\frac{37 308}{2,02} \approx 18 469\) hab/km² pour Monaco et \(d_2=\frac{126 477 000}{378 000} \approx 335\) hab/km² pour le Japon. Autrement dit, alors que la population de Monaco est la moins importante en taille, sa densité est plus importante que celle du Japon. (p. 11, modifié).
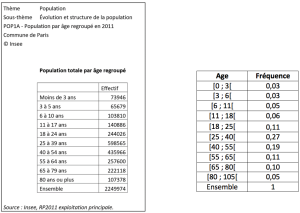
Ainsi, une représentation pertinente des populations de Monaco et du Japon doit rendre visible cette différence de densité. Il en est de même quand on cherche à représenter des fréquences de classes (notamment si elles sont d'amplitudes différentes) : il n'est pas pertinent, par exemple, de représenter de la même façon une fréquence égale à 0,05 de la classe \([6 ;11[\) et de la classe \([80 ;110[\). Ces deux classes d'âge ont la même fréquence mais l'amplitude de la première classe est très inférieure à celle de la seconde, on pressent donc que la densité de la première classe est supérieure à celle de la seconde. Par analogie avec la densité de population utilisée en géographie, on calculera le quotient de la fréquence d'une classe d'âge par l'amplitude de cette classe, et on parlera de densité de fréquence. Comme perçue, la densité de fréquence de la première tranche d'âge est plus grande que la densité de fréquence de la seconde tranche d'âge. La représentation graphique, qui n'est autre que l'histogramme, doit rendre visible ce phénomène. Nous proposons les définitions suivantes :
Un histogramme de fréquences est une représentation graphique composée de rectangles « collés » dont les aires sont proportionnelles aux fréquences et dont les bases sont déterminées par les intervalles des classes.
Dans le cas d'un caractère quantitatif continu, on définit la densité de fréquence \(d_i\) d'une classe de fréquence \(f_i\) et d'amplitude \(a_i\) par : \(d_i=\frac{f_i}{a_i}\).
Remarque :
On parle de caractère quantitatif continu, mais dans la majorité des cas, il s'agit d'un caractère quantitatif discret qui prend un grand nombre de valeurs et qu'il est alors plus intéressant de traiter les valeurs en classes comme pour un caractère quantitatif continu. C'est le cas dans cet exemple si l'on considère que l'âge de l'individu comptabilisé est celui à la date d'anniversaire de l'individu en 2011 (donc un nombre entier).
Nous trouvons donc que l'axe des ordonnées de l'histogramme représente la densité de fréquence (à constante multiplicative près), et non la fréquence comme on peut le voir très souvent dans les manuels. Bien entendu, fréquence et densité sont égales (ou tout du moins proportionnelles) lorsque les amplitudes des classes sont égales, mais l'histogramme n'a pas vocation à avoir toujours des classes d'amplitudes égales.
Il pourrait être envisagé la définition (plus rigoureuse mathématiquement) de l'histogramme suivante : un histogramme est la représentation graphique de la fonction \(d\) qui, à tout nombre réel \(x\) appartenant aux classes concernées par le phénomène étudié, associe la densité de fréquence \(d(x)\) de la classe à laquelle \(x\) appartient. La fonction d s'appelle la fonction de densité de fréquence de la série statistique étudiée. Cette formulation n'a pas été testée en classe.
Exercice à rendre : Tirage aléatoire
Cet exercice (à rendre) permet d'anticiper le problème du point mobile (séance suivante). Il travaille la simulation d' un nombre réel aléatoire sur un intervalle à l'aide du tableur et permet de rappeler certaines fonctionnalités du tableur. La notion d'histogramme est également réinvestie.
Cet exercice permet d'évoquer la fluctuation d'échantillonnage.
Fondamental : Institutionnalisation
A l'issue de cette séance, les élèves doivent être capable de construire et de comprendre ce que représente un histogramme.
Ils doivent retenir que l'axe des ordonnées d'un histogramme représente la densité de fréquence.